SHA256 compute in Verilog
On my last visit to the Embedded World, one of the most popular topics was Cyber Resilience Act and Cybersecurity, and FPGA had much to say in this area. They are fast, they can execute algorithms in parallel, and they are in the lower level of an ethernet interface checking all the packets, … summarizing, they are very involved in our cybersecurity. In this article, I want to focus on hash calculations, and we are going to see how we can implement a calculator of one of the most used hashes the SHA256.
A few weeks ago I implemented a SHA256 calculator in Verilog. The code is shared on Github. To verify that my SHA256 module computes well the hash, I used the webpage sha256algorithm.com, which explains step by step the SHA256 algorithm, and makes it perfect for debug the calculator.
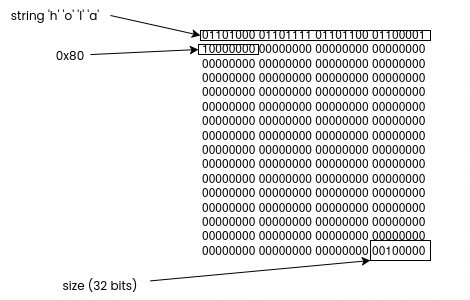
To calculate the SHA256, we need to work with three different vectors, the W, which is a vector of 64 words where the input data will be copied, the K vector, with 64 words which contains fixed values, and the A-H vector where the resulting hash will be stored. Firstly, we need to fill the W vector. The first step is to introduce the string we want to hash. The module I created calculates the SHA256 of a string up to 55 bytes or characters. The idea of this module is to calculate the hash of passwords, so with 56 characters it would be enough. SHA256 works with words of 32 bits and needs as input a set of 16 words. To introduce our password, we need to pack the characters into 32-bit words, using 14 of the 16 words for the input data. In addition, the next byte after the password will be configured with a fixed value of 0x80. Finally, the last two words (14 and 15), will be used to configure the size of the string. Since explaining this in words can be a little bit tricky, let’s see an example. For a string with the characters ‘h’, ‘o’, ‘l’, and ‘a’, the input words will be the next.
Once we have the first 16 words of the W vector, we need to compute the rest of the values until we fill the 64 words. The values in the words 16 to 64 will be calculated with the next equations.
w16 = w0 + σ0 + w9 + σ1
σ0 = (w1 rightrotate 7) xor (w1 rightrotate 18) xor (w1 rightshift 3)
σ1 = (w14 rightrotate 17) xor (w14 rightrotate 19) xor (w14 rightshift 10)
In Verilog, we can calculate the sigma variables with the next code.
assign theta0 = {w_array[w_index-15][6:0], w_array[w_index-15][31:7]} ^ {w_array[w_index-15][17:0], w_array[w_index-15][31:18]} ^ {3'b000, w_array[w_index-15][31:3]};
assign theta1 = {w_array[w_index-2][16:0], w_array[w_index-2][31:17]} ^ {w_array[w_index-2][18:0], w_array[w_index-2][31:19]} ^ {10'b0000000000, w_array[w_index-2][31:10]};
And the corresponding W value with the next code.
w_array[w_index] <= w_array[w_index-16] + theta0 + w_array[w_index-7] + theta1;
The module uses an AXI4 Stream Interface to receive the string using one transaction per character.

In order to detect the end of the string, the module detects the s_axis_tlast signal, and begins to compute the hash.
The complete code of the calculation of the W matrix is the next.
always @(posedge m_axis_aclk)
if (!m_axis_aresetn || (round == 7'd71)) begin
w_index <= 32'd0;
for (i=0; i < 63; i=i+1) begin
w_array[i] <= 32'd0;
end
message_complete <= 1'b0;
s_axis_tready <= 1'b1;
end
else begin
if (s_axis_tvalid && !message_complete) begin
w_array[w_index[10:5]][(31-w_index[4:0])-:8] <= s_axis_tdata[7:0];
if (s_axis_tlast) begin
w_array[w_index_1[10:5]][(31-w_index_1[4:0])-:8] <= 8'b10000000;
message_complete <= 1'b1;
w_index = 32'd16;
end
else begin
w_index <= w_index + 32'd8;
w_array[15] <= w_index + 32'd16;
end
end
else if (message_complete && (w_index < 32'd64)) begin
w_array[w_index] <= w_array[w_index-16] + theta0 + w_array[w_index-7] + theta1;
w_index <= w_index + 32'd1;
s_axis_tready <= 1'b0;
end
end
Now, we can begin the calculation of the hash itself by updating the content of the vector A-H over 64 rounds. The initial values of this vector are the values of the vector H, which is filled with fixed values that corresponds to the first 32 bits of the fractional parts of the square roots of the first 8 prime numbers.
localparam h0 = 32'b01101010000010011110011001100111;
localparam h1 = 32'b10111011011001111010111010000101;
localparam h2 = 32'b00111100011011101111001101110010;
localparam h3 = 32'b10100101010011111111010100111010;
localparam h4 = 32'b01010001000011100101001001111111;
localparam h5 = 32'b10011011000001010110100010001100;
localparam h6 = 32'b00011111100000111101100110101011;
localparam h7 = 32'b01011011111000001100110100011001;
The Verilog code for the initialization is the next.
if (!m_axis_aresetn || (!message_complete)) begin
round <= 7'd0;
a_reg <= h0;
b_reg <= h1;
c_reg <= h2;
d_reg <= h3;
e_reg <= h4;
f_reg <= h5;
g_reg <= h6;
h_reg <= h7;
hash <= 256'd0;
m_axis_tvalid <= 1'b0;
m_axis_tlast <= 1'b0;
end
Then, another vector we are going to need is K. The values of this vector are the first 32 bits of the fractional parts of the cube roots of the first 64 prime numbers, and the index used changes according to the current round.
/* return K according round */
assign k_round = (round == 7'd0)? k0:
(round == 7'd1)? k1:
(round == 7'd2)? k2:
(round == 7'd3)? k3:
(round == 7'd4)? k4:
(round == 7'd5)? k5:
(round == 7'd6)? k6:
(round == 7'd7)? k7:
(round == 7'd8)? k8:
(round == 7'd9)? k9:
...
(round == 7'd60)? k60:
(round == 7'd61)? k61:
(round == 7'd62)? k62:
k63;
Now, we need to update the values of the vector A-H according the next equations.
h = g
g = f
f = e
e = d + Temp1
d = c
c = b
b = a
a = Temp1 + Temp2
where
Temp1 = h + Σ1 + Choice + kn + wn
Temp2 = Σ0 + Majority
Σ1 = (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
Choice = (e and f) xor ((not e) and g)
Σ0 = (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
Majority = (a and b) xor (a and c) xor (b and c)
Being kn and wn the values of the W and K vectors for the current round. By configuring the W vector as a matrix in Verilog, this calculation can be implemented as memory reads.
At this point, the benefits of the FPGA make the difference. Note that, for the first update of the vector A-H, we need the value of the W[0], so we can parallelize the computation of the W and the A-H vectors since, when the input data is complete, we already have the values of the first 15 indexes of the W vector. By doing this, we reduce the number of clock cycles from 64*2 to 64+15, which are the first clock cycles used by data transmission.
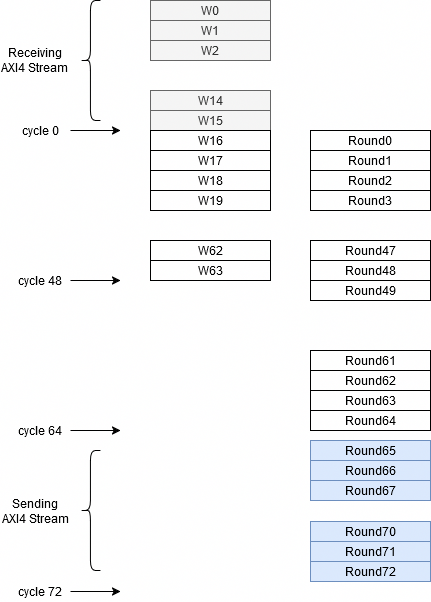
In the figure also there are 8 extra rounds to send the data over AXI4 Stream, but data is already calculated, and they can be sent using a parallel interface of 256 bits.
The code to make the calculations for the A-H vector is the next.
if (round < 64) begin
a_reg <= temp1 + temp2;
b_reg <= a_reg;
c_reg <= b_reg;
d_reg <= c_reg;
e_reg <= d_reg + temp1;
f_reg <= e_reg;
g_reg <= f_reg;
h_reg <= g_reg;
round <= round + 7'd1;
end
And here you can find the extra rounds needed to send the SHA256 calculated over AXI4 Stream.
m_axis_tdata <= (round == 64)? a_reg+h0:
(round == 65)? b_reg+h1:
(round == 66)? c_reg+h2:
(round == 67)? d_reg+h3:
(round == 68)? e_reg+h4:
(round == 69)? f_reg+h5:
(round == 70)? g_reg+h6:
h_reg+h7;
At this point, we have a module that computes the SHA256 of a string using the fewest clock cycles possible. In order to obtain the hash rate, we just need to calculate the number of hashes that the module is able to compute per second. Using a clock of 150 MHz, this module takes 64 cycles to compute the hash. We need to add a cycle to receive the data, and another one to send the data considering that the communications are parallelized. With these numbers, we have that each hash takes 440ns, which means a hash rate 2.27 MH/s. However, remember that we are using FPGA so we just need to replicate the module to increase the hash rate of this solution. Also, if we want to use several sha256 calculators in parallel, we need to implement a manager that activates and feeds each calculator.
Even the number 2.27 MH/s is not impressive compared with a regular GPU, what makes FPGA very interesting for the cybersecurity field is that we can use an embedded Linux OS on a single board computer while having a hash compute accelerator in parallel.